0 前言
作为前炉石/现游戏王玩家,经常看到这样的环境分析表:
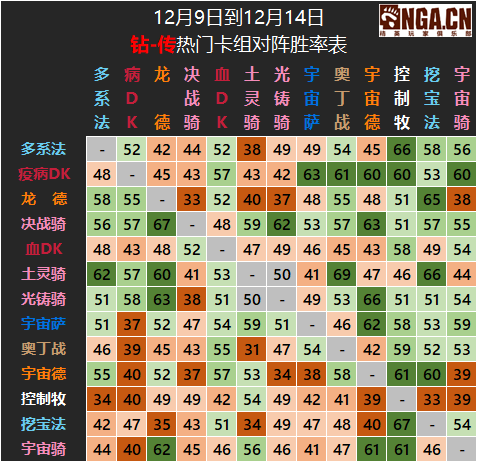

其中记述着卡组出场率或是卡组对战胜率表。那么根据这样的环境,我如何选择卡组,可以在环境中有更高的获胜希望呢?如果当所有玩家都尽可能地选择更高获胜期望的策略,那么环境最终会稳定吗?
1 完全信息静态博弈
我摘录一下书中的定义:
完全信息:所有参与者清楚地了解与博弈有关的所有信息。
静态:博弈者同时行动,或行动时不知晓对方的行动。
完全信息静态博弈:同时满足以上两个条件。
尽管每个卡组的胜率还跟不同玩家、先后手有关系,为了简化模型,假设所有玩家都是极高水平,那么卡组之间的胜率便是已知信息。而在选择卡组时,玩家们是不会预先知道对手使用的是什么卡组,那么就满足了静态条件。因此,这便是一个完全信息静态博弈过程。
2 Nash均衡
Nash定理告诉我们,对于这样的有限博弈过程,至少存在一个Nash均衡。在Nash均衡下,所有参与者无论其他人如何选择,他们均不会更换策略。
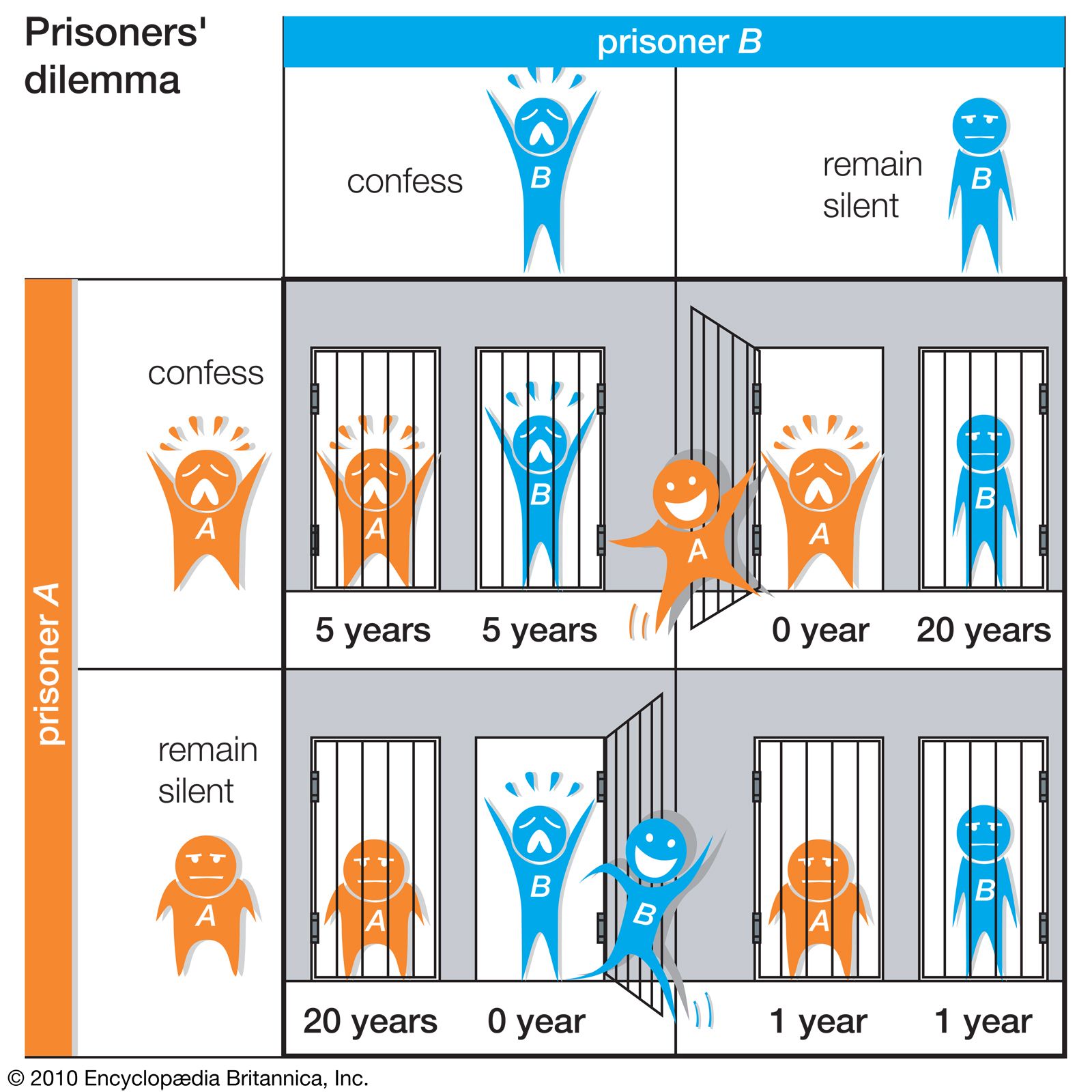
被提及最多的Nash均衡例子便是囚徒博弈,一个囚徒在选择招供的情况下,无论另一个囚徒选择什么,他都能相对于沉默获得更多收益。
这被称之为纯策略的纳什均衡,他有一个必定的选择。但有的时候不存在这样必定的选择,比如——
3 石头、剪刀、布的环境平衡
我们来看一个最简单的环境例子,即只有互相克制的三种卡组,卡组之间内战胜率为50%。这很像“石头、剪刀、布”的游戏,只不过规定猜拳结果相同下随机决定胜负。
胜率表可以用P矩阵来表示,$p_ij$表示使用$i$卡组对战$j$卡组的胜率,1石头、2剪刀、3布:
| vs | 石头 | 剪刀 | 布 |
|---|---|---|---|
| 石头 | 0.5 | 1 | 0 |
| 剪刀 | 0 | 0.5 | 1 |
| 布 | 1 | 0 | 0.5 |
假设赢得游戏收益为1,输掉游戏收益为-1,那么可以得到收益期望矩阵E
不难得出,收益的期望$e_{ij} = p_{ij} − (1−p_{ij}) = 2p_{ij} − 1$
| vs | 石头 | 剪刀 | 布 |
|---|---|---|---|
| 石头 | 0 | 1 | -1 |
| 剪刀 | -1 | 0 | 1 |
| 布 | 1 | -1 | 0 |
这时候,就要用到混合策略纳什均衡,我既不是100%出石头也不是100%出剪刀,而是以1/3 的概率出石头/剪刀/布。假设对手只出石头,那么收益为:
$1/3 * 0 +1/3 * (−1)+1/3 * 1 = 0$
同理,对手只出剪刀、布收益仍为0,并且就算对手也采取混合策略,收益还是0。这种情况下,无论对手选取何种策略, 收益均不会变小,因此达到了一个Nash均衡点。由于这个游戏对于双方是可交换的,因此双方的Nash均衡策略为:$1/3$出石头、$1/3$出剪刀、$1/3$出布。
4 Nash均衡的求解
在上一节直接给出了Nash均衡点,而且是来源于经验、显而易见的。那对于复杂的环境,如何求解呢?
假设环境中的n个卡组胜率矩阵$P$表示如下:
| vs | 卡组1 | 卡组2 | 卡组3 | … | 卡组n |
|---|---|---|---|---|---|
| 卡组1 | 0.5 | $p_{12}$ | $p_{13}$ | ... | $p_{1n}$ |
| 卡组2 | $p_{21}$ | 0.5 | ... | ... | ... |
| 卡组3 | $p_{31}$ | ... | 0.5 | ... | ... |
| ... | ... | ... | ... | ... | ... |
| 卡组n | $p_{n1}$ | ... | ... | ... | 0.5 |
对称性:$p_{ij} + p_{ji} = 1$
另外,这还是一个零和博弈,无论双方选择什么策略,期望和必定为0:
$\forall S_a,S_b : E_a + E_b = 0$
又由于玩家a和b是可交换的,即他们都采取使自己期望收益最大的策略,其期望相等:
$max E_a = max E_b$
由此可知
$max E_a = max E_b = 0$
即Nash均衡点,也就是双方采取最佳策略的情况下,收益为0
假设玩家a采取混合策略$α = [a_1 a_2…]^T$,玩家b采用混合策略$β = [b_1 b_2…]^T$,则玩家a的期望收益为:
$E_a = α^T E β$
混合策略为Nash均衡策略时,无论a采取什么策略,b均收益为0,则达到Nash均衡点,即
$∀α : α^T E β =0$
因此
$E β =0$
再联立
$\sum_{n}^{i=1} b_i = 1$
得到非齐次线性方程组:
$\begin{bmatrix} E \\ 1 \end{bmatrix} \boldsymbol{\beta}
=
\begin{bmatrix} \boldsymbol{0} \\ 1 \end{bmatrix}$
便可解出Nash均衡结果,由对称性也可得$α=β$。
5 一个简单的例子
我们以炉石传说中经典模式(虽然已经没了)的奇迹贼、动物园、防战为例:
胜率矩阵P:
| vs | 1奇迹贼 | 2动物园 | 3防战 |
|---|---|---|---|
| 1奇迹贼 | 0.5 | 0.51 | 0.49 |
| 2动物园 | 0.49 | 0.5 | 0.54 |
| 3防战 | 0.51 | 0.46 | 0.5 |
收益矩阵E:
| vs | 1奇迹贼 | 2动物园 | 3防战 |
|---|---|---|---|
| 1奇迹贼 | 0 | 0.02 | -0.02 |
| 2动物园 | -0.02 | 0 | 0.08 |
| 3防战 | 0.02 | -0.08 | 0 |
方程组:
$\begin{bmatrix} 0&0.02&-0.02 \\ -0.02&0&0.08 \\0.02&-0.08&0 \\ 1&1&1 \end{bmatrix}
\begin{bmatrix} b_1 \\ b_2 \\ b_3 \end{bmatrix}
=
\begin{bmatrix} 0 \\ 0 \\ 0 \\ 1 \end{bmatrix}$
解得:
$\begin{bmatrix} b_1 , b_2 , b_3 \end{bmatrix}
=
\begin{bmatrix} 2/3 , 1/6 , 1/6 \end{bmatrix}$
于是环境中有2/3的奇迹贼,1/6的动物园,1/6的防战是均衡的。




0 条评论