AES简介
AES全称Advanced Encryption Standard,即高级加密标准。它是一种广为使用的对称加密方法,所谓对称加密就是加密和解密使用的是相同的密钥。这种加密方法是按照块加密的,每一个被加密的块是128bit(16B);加密用的密钥可以为128/192/256bit(16/24/32B),使用的密钥不同,加密的循环轮数不同,128位密钥为10轮,192位密钥为12轮,256位密钥为14轮;加密的结果为128bit(16B)。
要理解AES中的计算过程,首先要了解有限域的运算知识:
有限域
域和有限域
首先给域下一个定义,由于本文不想写得太过复杂,所以可能不是很严格。简单来说,一个域就是定义了加法和乘法的集合,且满足以下条件:
1、加法是封闭的,非零元素乘法是封闭的。
$\forall a,b\in F: a+b\in F;\forall a,b\in F-\{0\}: a*b\in F-\{0\}$
2、加法和乘法有单位元和逆元,加法单位元记为0,乘法单位元记为1。
$a+0=a, a*1=a$
$\forall a\in F, \exists b\in F: a+b=0;\forall a\in F-\{0\},\exists b\in F-\{0\}: a*b=1$
有了逆元的概念,其实我们也可以定义减法和除法了,减法即+加法逆元,除法即x乘法逆元。
3、加法有交换律、结合律。
$a+b=b+a,a+(b+c)=(a+b)+c$
4、乘法有交换律、结合律,加法与乘法之间有分配律。
$a*b=b*a,a*(b*c)=(a*b)*c,a*(b+c)=a*b+a*c$
我们熟知的数域(例如:有理数域Q、实数域R)显然是满足以上条件的,但数域中元素的个数是无限的,如果我们要在有限的元素中定义一个域呢?
先看一个简单的例子,$GF(3)$即有三个元素0、1、2的有限域,我们如果把加法和乘法定义为模3的加法和乘法,那么就满足域的条件了。
例如:
$(1 + 2) mod 3 = 0$
$(2 * 2) mod 3 = 1$
同时也可看出,1的加法逆元是2,2的乘法逆元是2。
实际上,有限域元素的个数是限定的,记为$GF(p^n)$,p为质数,n为正整数。即有限域元素的个数必定是质数的正整数幂$p^n$。对于$GF(p)$的情况,加法和乘法定义就像上面的$GF(3)$一样,是模p的加法和乘法,就能满足域的条件。但对于$GF(p^n)$的加法和乘法就不一样了。
例如AES算法中用到的$GF(2^8)$,如果还定义为模256的加法和乘法,会出现$(16 * 16) mod 256 = 0$,这与第1个条件,非零元素的乘法封闭性相悖。那我们如何定义$GF(2^8)$的加法和乘法呢?
多项式
这就要用到多项式了,我们将$GF(2^8)$表达为多项式,多项式的加法和乘法就会满足域的定义。例如42的2进制表达为$(101010)_2$,那么42就代表多项式$1x^5+0x^4+1x^3+0x^2+1x^1+0$,也就是小于256的数表达为多项式的系数。
假设我们要计算42+12,就把多项式对应项系数相加,系数的加法遵循$GF(2)$中的加法,即:
$(1x^5+0x^4+1x^3+0x^2+1x^1+0) + (1x^3+1x^2+0x^1+0) = 1x^5+0x^4+0x^3+1x^2+1x^1+0$
也就是$42+12=(100110)_2=38$。可以发现,其实$GF(2^8)$中的加法,就是两个二进制数的异或运算结果。
对于乘法,两个最高次<8的多项式可能乘出一个最高次>8的多项式(例如$x^7 * x^7 = x^{14} $),这不是不满足乘法的封闭性了吗?所以,对于$GF(2^8)$中的乘法,我们需要模一个不可约的多项式$x^8+x^4+x^3+x^1+1$,这样就能保证乘法的结果也在256的范围内。那么这就牵涉到另一个问题,多项式如何做带余除法呢?参照整数带余除法的定义,我们有:
如果$a(X) = q(X)b(X) + r(X)$,且$r(X)$的最高次数<$b(X)$的最高次数,那么称$a(X)$除以$b(X)$商$q(X)$余$r(X)$。
例如我们要计算$GF(2^8)$中的128*128,即$(x^7 * x^7) mod (x^8+x^4+x^3+x^1+1)$:
$\begin{align}
& \underline{x^6+x^2+x} \\
x^8+x^4+x^3+x+1) & x^{14} \\
& \underline{x^{14}+x^{10}+x^9+x^7+x^6+x^4} \\
& x^{10}+x^9+x^7+x^6+x^4 \\
& \underline{x^{10}+x^6+x^5+x^3+x^2} \\
& x^9+x^7+x^5+x^3+x^2 \\
& \underline{x^9+x^5+x^4+x^2+x} \\
& x^7+x^4+x^3+x
\end{align}$
即$x^{14}$除以$x^8+x^4+x^3+x^1+1$:商$x^6+x^2+x$,余$x^7+x^4+x^3+x$。
将$x^7+x^4+x^3+x$转换为二进制是${(1001 1010)}_2$即0x9a,也就是0x80*0x80=0x9a。
因此,对于$GF(2^8)$,我们有了新的加法和乘法定义:对应多项式的加法和$mod (x^8+x^4+x^3+x^1+1)$乘法,其中多项式系数的加法和乘法遵循$GF(2)$的加法和乘法,即mod 2的加法和乘法。这样的加法和乘法定义,使得它满足域的条件。
AES算法
AES算法是以块为单位进行的,例如一个128bit的块可以表示为:
$\begin{bmatrix}
00 & 04 & 08 & 0c\\
01 & 05 & 09 & 0d\\
02 & 06 & 0a & 0e\\
03 & 07 & 0b & 0f\\
\end{bmatrix}$
我们以128bit的块和密钥加密为例,加密分为加初始轮密钥、10轮循环。每轮循环中,包含S盒变换、行位移、列混合、加轮密钥4个步骤,并且最后一轮循环不再列混合操作,可以记为如下几个步骤:
0、加初始轮密钥K[0]
重复1234循环,9轮:
1、S盒变换
2、行位移
3、列混合
4、加本轮密钥K[i]
再重复124,1轮,即共10轮循环。
对于这些步骤具体的操作如下:
1 S盒变换
S盒变换遵循以下公式:
$\boldsymbol{y}=\boldsymbol{A}\boldsymbol{x}^{-1}+\boldsymbol{b}$
其中
$\boldsymbol{A} = \begin{bmatrix}
1 & 1 & 1 & 1 & 1 & 0 & 0 & 0\\
0 & 1 & 1 & 1 & 1 & 1 & 0 & 0\\
0 & 0 & 1 & 1 & 1 & 1 & 1 & 0\\
0 & 0 & 0 & 1 & 1 & 1 & 1 & 1\\
1 & 0 & 0 & 0 & 1 & 1 & 1 & 1\\
1 & 1 & 0 & 0 & 0 & 1 & 1 & 1\\
1 & 1 & 1 & 0 & 0 & 0 & 1 & 1\\
1 & 1 & 1 & 1 & 0 & 0 & 0 & 1\\
\end{bmatrix}, \boldsymbol{b} = \begin{bmatrix} 0 & 1 & 1 & 0 & 0 & 0 & 1 & 1 \end{bmatrix}^T$
也就是先对原来的值求逆,再左乘变换矩阵$\boldsymbol{A}$,可以看出$\boldsymbol{A}$实际上是0xf8的循环移位。然后再加上$\boldsymbol{b}$,这里的加法仍然是mod 2的加法,也就是与0x63进行异或运算。另外在$GF(2^8)$中,0是没有逆元素的,但在这里为了让每个值都在S盒变换后有值,因此这里定义$0^{-1}=0$,也就是0x00会变换为0x63。这样就保证了每一个字节经过S盒变换变为另一个字节,变换前后的值是一一对应的,因此S盒变换也是可逆的。
由于S盒变换中有求逆的步骤,比较复杂,因此事先生成好S盒变换表,即可根据原值找到S盒变换后的值。同样的,在生成S盒变换表时,同时也生成一个S盒逆变换的表,便于解密过程。
S盒变换表:
0 1 2 3 4 5 6 7 8 9 a b c d e f
0 63 7c 77 7b f2 6b 6f c5 30 01 67 2b fe d7 ab 76
1 ca 82 c9 7d fa 59 47 f0 ad d4 a2 af 9c a4 72 c0
2 b7 fd 93 26 36 3f f7 cc 34 a5 e5 f1 71 d8 31 15
3 04 c7 23 c3 18 96 05 9a 07 12 80 e2 eb 27 b2 75
4 09 83 2c 1a 1b 6e 5a a0 52 3b d6 b3 29 e3 2f 84
5 53 d1 00 ed 20 fc b1 5b 6a cb be 39 4a 4c 58 cf
6 d0 ef aa fb 43 4d 33 85 45 f9 02 7f 50 3c 9f a8
7 51 a3 40 8f 92 9d 38 f5 bc b6 da 21 10 ff f3 d2
8 cd 0c 13 ec 5f 97 44 17 c4 a7 7e 3d 64 5d 19 73
9 60 81 4f dc 22 2a 90 88 46 ee b8 14 de 5e 0b db
a e0 32 3a 0a 49 06 24 5c c2 d3 ac 62 91 95 e4 79
b e7 c8 37 6d 8d d5 4e a9 6c 56 f4 ea 65 7a ae 08
c ba 78 25 2e 1c a6 b4 c6 e8 dd 74 1f 4b bd 8b 8a
d 70 3e b5 66 48 03 f6 0e 61 35 57 b9 86 c1 1d 9e
e e1 f8 98 11 69 d9 8e 94 9b 1e 87 e9 ce 55 28 df
f 8c a1 89 0d bf e6 42 68 41 99 2d 0f b0 54 bb 16逆变换表:
0 1 2 3 4 5 6 7 8 9 a b c d e f
0 52 09 6a d5 30 36 a5 38 bf 40 a3 9e 81 f3 d7 fb
1 7c e3 39 82 9b 2f ff 87 34 8e 43 44 c4 de e9 cb
2 54 7b 94 32 a6 c2 23 3d ee 4c 95 0b 42 fa c3 4e
3 08 2e a1 66 28 d9 24 b2 76 5b a2 49 6d 8b d1 25
4 72 f8 f6 64 86 68 98 16 d4 a4 5c cc 5d 65 b6 92
5 6c 70 48 50 fd ed b9 da 5e 15 46 57 a7 8d 9d 84
6 90 d8 ab 00 8c bc d3 0a f7 e4 58 05 b8 b3 45 06
7 d0 2c 1e 8f ca 3f 0f 02 c1 af bd 03 01 13 8a 6b
8 3a 91 11 41 4f 67 dc ea 97 f2 cf ce f0 b4 e6 73
9 96 ac 74 22 e7 ad 35 85 e2 f9 37 e8 1c 75 df 6e
a 47 f1 1a 71 1d 29 c5 89 6f b7 62 0e aa 18 be 1b
b fc 56 3e 4b c6 d2 79 20 9a db c0 fe 78 cd 5a f4
c 1f dd a8 33 88 07 c7 31 b1 12 10 59 27 80 ec 5f
d 60 51 7f a9 19 b5 4a 0d 2d e5 7a 9f 93 c9 9c ef
e a0 e0 3b 4d ae 2a f5 b0 c8 eb bb 3c 83 53 99 61
f 17 2b 04 7e ba 77 d6 26 e1 69 14 63 55 21 0c 7d查表方式:左边每行开头为高位,上边每列开头为低位,例如4b查第一个表得b3,用b3查第二个表得4b。
2 行位移
行位移可以用下面的矩阵作为例子,即第一行不动,第二行循环左移1个字节,第三行2个,第四行3个。
$\begin{bmatrix}
00 & 04 & 08 & 0c\\
\color{red}{01} & 05 & 09 & 0d\\
\color{red}{02} & \color{red}{06} & 0a & 0e\\
\color{red}{03} & \color{red}{07} & \color{red}{0b} & 0f\\
\end{bmatrix}
\rightarrow
\begin{bmatrix}
& & & 00 & 04 & 08 & 0c\\
& & \color{red}{01} & 05 & 09 & 0d & <<1\\
& \color{red}{02} & \color{red}{06} & 0a & 0e & & <<2\\
\color{red}{03} & \color{red}{07} & \color{red}{0b} & 0f & & & <<3\\
\end{bmatrix}
\rightarrow
\begin{bmatrix}
00 & 04 & 08 & 0c\\
05 & 09 & 0d & \color{red}{01}\\
0a & 0e & \color{red}{02} & \color{red}{06}\\
0f & \color{red}{03} & \color{red}{07} & \color{red}{0b}\\
\end{bmatrix}$
3 列混合
列混合是用整个块左乘一个变换矩阵,由于$GF(2^8)$中的乘法是可逆的,所以这一步也是可逆的,逆变换左乘一个逆矩阵即可。
列混合:
$Y=\begin{bmatrix}
2 & 3 & 1 & 1\\
1 & 2 & 3 & 1\\
1 & 1 & 2 & 1\\
3 & 1 & 1 & 2\\
\end{bmatrix}X$
逆列混合:
$X=\begin{bmatrix}
e & b & d & 9\\
9 & e & b & d\\
d & 9 & e & b\\
b & d & 9 & e\\
\end{bmatrix}Y$
(注意,这里的矩阵相乘运算用到的是$GF(2^8)$中的加法和乘法。)
4 加轮密钥
初始轮加的密钥为$K_0$,即原始密钥,之后每一轮加的密钥由前一轮的密钥变换而来。这一步可以表示为块和密钥相加:
$Y=X+K_i$
(注意,这里的加法仍然是遵循$GF(2^8)$中的加法,即异或。)
密钥的生成算法如下:
设前一轮的密钥表示为:
$K_{i-1}=\begin{bmatrix}
k_0 & k_4 & k_8 & k_c\\
k_1 & k_5 & k_9 & k_d\\
k_2 & k_6 & k_a & k_e\\
k_3 & k_7 & k_b & k_f\\
\end{bmatrix}$
取最后一列,进行循环移位、S盒变换、加${Rcon}_i$,再与第一列异或得到后一轮密钥的第一列
$\begin{bmatrix}
\color{red}{k_c}\\
k_d\\
k_e\\
k_f\\
\end{bmatrix}
\stackrel{循环上移}{\longrightarrow}
\begin{bmatrix}
k_d\\
k_e\\
k_f\\
\color{red}{k_c}\\
\end{bmatrix}
\stackrel{S盒变换}{\longrightarrow}
\begin{bmatrix}
S(k_d)\\
S(k_e)\\
S(k_f)\\
S(k_c)\\
\end{bmatrix}
\stackrel{+{Rcon}_i}{\longrightarrow}
\begin{bmatrix}
S(k_d)+{Rcon}_i\\
S(k_e)\\
S(k_f)\\
S(k_c)\\
\end{bmatrix}
\stackrel{+第1列}{\longrightarrow}
\begin{bmatrix}
k_0+S(k_d)+{Rcon}_i\\
k_1+S(k_e)\\
k_2+S(k_f)\\
k_3+S(k_c)\\
\end{bmatrix}
\stackrel{记为}{=}
\begin{bmatrix}
l_0\\
l_1\\
l_2\\
l_3\\
\end{bmatrix}$
其中${Rcon}_i=2^{i-1}$,算法遵循$GF(2^8)$中的乘法,可以得到(均为16进制):
$\{{Rcon}_i\}=\{01,02,04,08,10,20,40,80,1b,36\}$
之后3列用原来的列和前一列相加得到:
$K_i=\begin{bmatrix}
l_0 & l_4 & l_8 & l_c\\
l_1 & l_5 & l_9 & l_d\\
l_2 & l_6 & l_a & l_e\\
l_3 & l_7 & l_b & l_f\\
\end{bmatrix}=\begin{bmatrix}
l_0 & k_4+l_0 & k_8+l_4 & k_c+l_8\\
l_1 & k_5+l_1 & k_9+l_5 & k_d+l_9\\
l_2 & k_6+l_2 & k_a+l_6 & k_e+l_a\\
l_3 & k_7+l_3 & k_b+l_7 & k_f+l_b\\
\end{bmatrix}$
可以写为一个总的密钥变换公式:
$K_i=f(K_{i-1})=f(\begin{bmatrix}
k_0 & k_4 & k_8 & k_c\\
k_1 & k_5 & k_9 & k_d\\
k_2 & k_6 & k_a & k_e\\
k_3 & k_7 & k_b & k_f\\
\end{bmatrix})$
$=\small{\begin{bmatrix}
k_0+S(k_d)+{Rcon}_i & k_4+k_0+S(k_d)+{Rcon}_i & k_8+k_4+k_0+S(k_d)+{Rcon}_i & k_c+k_4+k_0+S(k_d)+{Rcon}_i\\
k_1+S(k_e) & k_5+k_1+S(k_e) & k_9+k_5+k_1+S(k_e) & k_d+k_9+k_5+k_1+S(k_e)\\
k_2+S(k_f) & k_6+k_2+S(k_f) & k_a+k_6+k_2+S(k_f) & k_e+k_a+k_6+k_2+S(k_f)\\
k_3+S(k_c) & k_7+k_3+S(k_c) & k_b+k_7+k_3+S(k_c) & k_f+k_b+k_7+k_3+S(k_c)\\
\end{bmatrix}}$
举个例子
前面叙述了完整的加密过程,但比较抽象,这里举个简单的例子,设原文为$P$,加密密钥为$K=K_0$,加密结果为$C$。
$P=\begin{bmatrix}
32 & 88 & 31 & e0\\
43 & 5a & 31 & 37\\
f6 & 30 & 98 & 07\\
a8 & 8d & a2 & 34\\
\end{bmatrix},K_0=\begin{bmatrix}
2b & 28 & ab & 09\\
7e & ae & f7 & cf\\
15 & d2 & 15 & 4f\\
16 & a6 & 88 & 3c\\
\end{bmatrix}$
0、首先加初始轮密钥,也就是计算$C=P+K_0$,例如第一行第一列就是0x32+0x2b=0x19,即异或运算:
$C=P+K_0=\begin{bmatrix}
19 & a0 & 9a & e9\\
3d & f4 & c6 & f8\\
e3 & e2 & 8d & 48\\
be & 2b & 2a & 08\\
\end{bmatrix}$
1、查S盒变换表,对每个字节进行变换,例如0x19查表得0xd4:
$C=S(C)=\begin{bmatrix}
d4 & e0 & b8 & 1e\\
27 & bf & b4 & 41\\
11 & 98 & 5d & 52\\
ae & f1 & e5 & 30\\
\end{bmatrix}$
2、行位移,第一行不动,后面三行依次循环左移1/2/3个字节:
$\begin{bmatrix}
d4 & e0 & b8 & 1e\\
27 & bf & b4 & 41\\
11 & 98 & 5d & 52\\
ae & f1 & e5 & 30\\
\end{bmatrix}\rightarrow\begin{bmatrix}
d4 & e0 & b8 & 1e\\
bf & b4 & 41 & 27\\
5d & 52 & 11 & 98\\
30 & ae & f1 & e5\\
\end{bmatrix}$
3、列混合,左乘变换矩阵,得变换后的矩阵,例如第一行第一列的计算:2*d4+3*bf+5d+30 = b3+da+5d+30 = 04
$C=\begin{bmatrix}
2 & 3 & 1 & 1\\
1 & 2 & 3 & 1\\
1 & 1 & 2 & 1\\
3 & 1 & 1 & 2\\
\end{bmatrix}\begin{bmatrix}
d4 & e0 & b8 & 1e\\
bf & b4 & 41 & 27\\
5d & 52 & 11 & 98\\
30 & ae & f1 & e5\\
\end{bmatrix}=\begin{bmatrix}
04 & e0 & 48 & 28\\
66 & cb & f8 & 06\\
81 & 19 & d3 & 26\\
e5 & 9a & 7a & 4c\\
\end{bmatrix}$
4、加轮密钥,首先根据变换公式,生成本轮的密钥$K_1$:
第1列$\begin{bmatrix}
k_0+S(k_d)+{Rcon}_i\\
k_1+S(k_e)\\
k_2+S(k_f)\\
k_3+S(k_c)\\
\end{bmatrix}=\begin{bmatrix}
2b+S(cf)+01\\
7e+S(4f)\\
15+S(3c)\\
16+S(09)\\
\end{bmatrix}=\begin{bmatrix}
a0\\
fa\\
fe\\
17\\
\end{bmatrix}$
然后依次得第2~4列:$\begin{bmatrix}
a0 & 28+a0=88 & ab+88=23 & 09+23=2a\\
fa & ae+fa=54 & f7+54=a3 & cf+a3=6c\\
fe & d2+fe=2c & 15+2c=39 & 4f+39=76\\
17 & a6+17=b1 & 88+b1=39 & 3c+39=05\\
\end{bmatrix}$
再将密文加上本轮的密钥:
$C=\begin{bmatrix}
04 & e0 & 48 & 28\\
66 & cb & f8 & 06\\
81 & 19 & d3 & 26\\
e5 & 9a & 7a & 4c\\
\end{bmatrix}+\begin{bmatrix}
a0 & 88 & 23 & 2a\\
fa & 54 & a3 & 6c\\
fe & 2c & 39 & 76\\
17 & b1 & 39 & 05\\
\end{bmatrix}=\begin{bmatrix}
a4 & 68 & 6b & 02\\
9c & 9f & 5b & 6a\\
7f & 35 & ea & 50\\
f2 & 2b & 43 & 49\\
\end{bmatrix}$
然后再重复以上1234步,总共进行9轮,再进行没有3 列混合步骤的第10轮,即得密文:
$\begin{bmatrix}
39 & 02 & dc & 19\\
25 & dc & 11 & 6a\\
84 & 09 & 85 & 0b\\
1d & fb & 97 & 32\\
\end{bmatrix}$
图解过程
画了一张长图涵盖了上述过程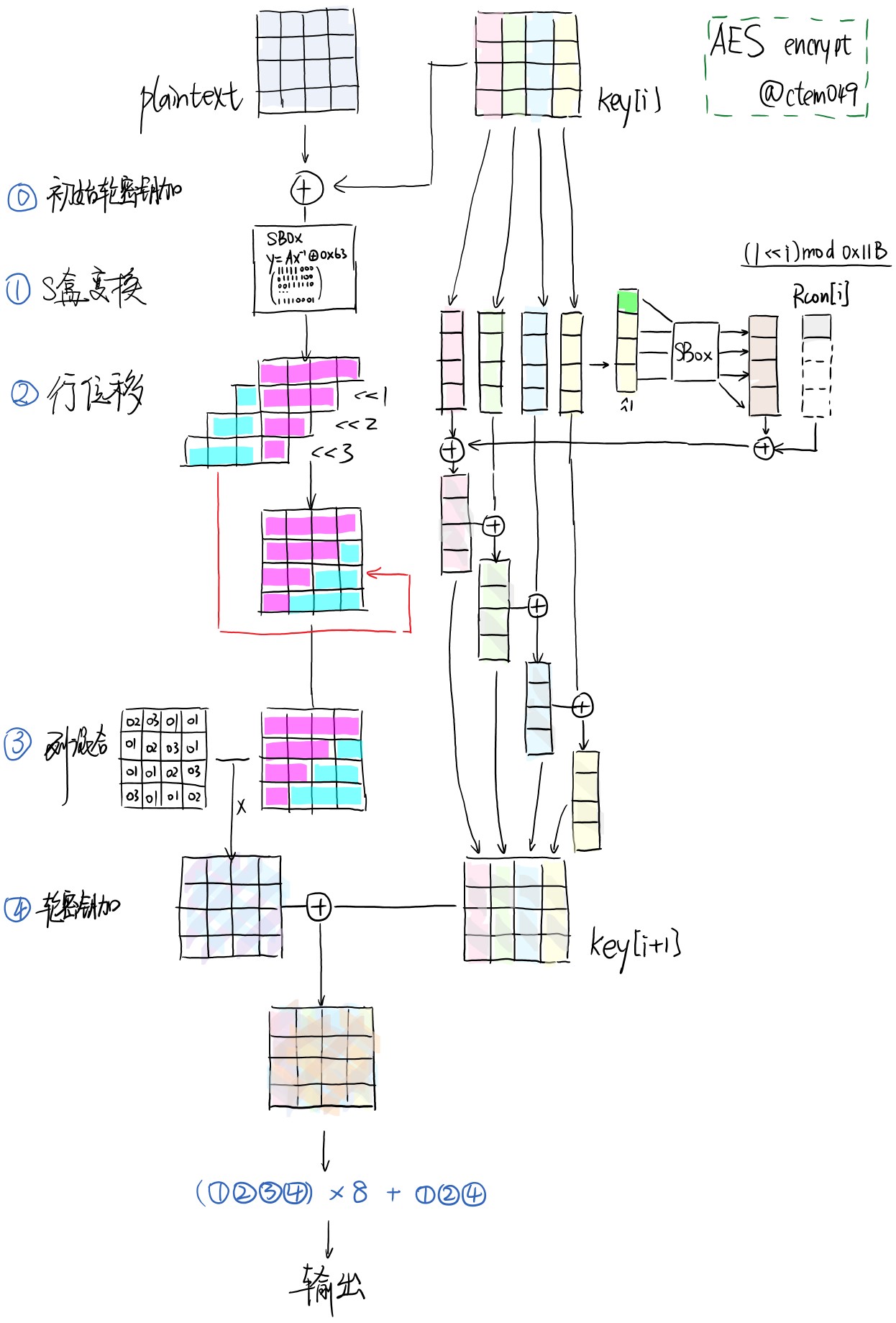




本文的翻译结果:
可怕的科学:密码全攻略
By billy at 2021-01-20 16:38:27.
厉害呢.jpg
By 草苺奶昔 at 2021-01-19 19:04:26.